Monogatari Series - Volume Ex - Chapter 7

007 

Using a shogi board to represent multiplication tables was a blind spot for me as a pro, or rather, it was completely unexpected, but I didn’t feel it was that surprising. Even if you couldn’t really say that 4 × 4 = 16 comes from the other word for lion, it sometimes happens that the shogi board itself is expressed as 9 × 9 = 81. Also, there was proper foreshadowing in Hanekawa-san’s story—Oikura-san’s hobby wasn’t shogi, but math.  

By the way, math also happens to be my best subject. 

“Right. Just what I would expect from someone with the name 

Rei.”  

“No, my name isn’t the reason that I’m good at math though?” 

“Well then Kiriyama-kun, maybe you would get along with Oikurasan.” 

“What’s this? Why have you suddenly started telling scary stories, Hanekawa-san?” 

Also, times tables aren’t math, it’s in the realm of arithmetic for second graders. 

The classroom wall was probably the classroom wall from when she was in the second grade of elementary school.  

Certainly, this kind of chart was stuck to the wall—how about that? 

Are we right back at “so what?”? 

Should I discard it as the strained interpretations of an amateur?— No, I felt. 

As I thought, we still hadn’t cleared anything up, but I had a feeling it fit perfectly. This was an intuitive choice of words that would get me scolded by Shimada-san again, but I had a hunch that her way of thinking was right.  

Why did I have that hunch? 

Dig down. Reach out your hand. Grab it. 

That’s right. 

Because if we take it as a multiplication table, the positions of the arranged pieces was miraculous.  

“Miraculous? Meaning?” 

“Look, Hanekawa-san. The positions of all of the pieces are all in the odd number squares of the multiplication table.” 

At first we explained it as the pieces being arranged “to fill in the spaces of a grid pattern” and lining it up with the new multiplication table, and if you overlay them, a completely different aspect presents itself. 

In other words, this. 

I borrowed the chalk from Hanekawa-san and added more lines to the multiplication table on the ground. 

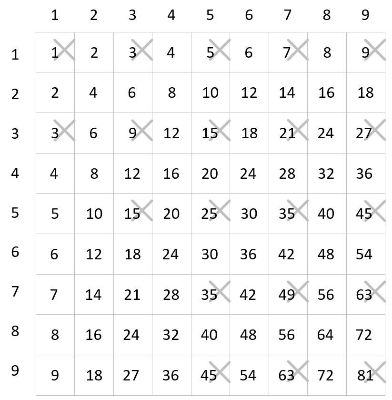
I was finally fully participating in the street art activities. Even though it was just crossing out numbers, I explained it as me trying to wipe away that embarrassment. 

“I don’t think the kinds of pieces are related. They just wanted twenty pieces to cover twenty odd numbers.” 

If the pieces were arranged with that goal in mind, and if they scattered around twenty more pieces from the white player to make it harder to figure out, it wasn’t impossible for it to end up in a distorted board state— 

Far from it, so much so that if it wasn’t like that it would be strange.  If anything, you can also look at it as the sender badly staged this impossible, or rather this insulting, borderline blasphemous, arrangement of pieces to help the receiver notice that. 

But there were still some questions remaining. 

Why did Oikura-san’s correspondence partner send a game board that hinted at “odd numbers”? Their intentions were still a mystery. Intentions aside, even if our reasoning was on the mark, I would have to point out that it wasn’t complete.  

All of the odd numbers not being covered made it incomplete. 

Mathematically speaking, it wasn’t beautiful. 

If you wanted to cover odd numbers, or if you wanted to highlight the odd numbers, why wouldn’t you cover all twenty-five of the odd numbers that appear on a multiplication table? 

“The odd numbers on a multiplication table are 1, 3, 3, 5, 5, 7, 7, 9, 9, 9, 15, 15, 21, 21, 25, 27, 27, 35, 35, 45, 45, 49, 63, 63, 81. Fourteen numbers in twenty-five pairs. And on this game board, five numbers and five spaces that are not covered by black pieces are 5, 7, 9, 21, 27— there doesn’t seem to be any special progression, does there?” As usual, Hanekawa-san confirmed this out loud. 

Delightful, like she was humming a song. 5, 7, 9, 21, 27. 

There was no common divisor. You couldn’t even say they were all primes. No arithmetic progression, either. If you add 5, 7, and 9 together you get 21, but you couldn’t really explain its relationship with 27. 

We should think of the thing these numbers have in common is that they are on the left corner of the multiplication table after all—the lower-left corner of the board and the left corner of the multiplication table. 

“But if we look at it like this, at the lower-left corner ‘5×1’ sticks out—or if there wasn’t a piece at the ‘9×5’ area, I feel the overall balance would be good.” 

What Hanekawa-san said felt a little sloppy, but my opinion was the same—I felt there was one piece too many, or one too few. 

Then let’s think of it the other way around. 

What rule should we find to feel like this empty space is “just right”? 

Hold on. The “5×1” area… The “9×5” area. 

Even though I had the same opinion as Hanekawa-san, just the expression itself felt slightly out of place. A sense of feeling out of place was also an intuitive thing, after all. 

“…… Hanekawa-san. Could you talk a little bit more? Anything is fine.” 

“Hmm. Hmm. What’s with that? That’s really putting me on the spot, don’t you think?” Although Hanekawa-san said that, she kept going without asking “why?”. 

“To put it another way, even though the ‘5’ in the ‘5×1’ area isn’t covered, the ‘5’ in the ‘1×5’ area is, why is that? They’re both ‘5’, so then to the pen-pal ‘5×1’ and ‘1×5’ must have different meanings.” Just as if she were talking to herself. 

Unfortunately, the answer to that muttered question of whether or not there was a difference in meaning, didn’t set off any flashes of insight inside me—instead, something else flashed. 

That’s right. 

I know the identity of this sense of unease. Precisely. 

“Hanekawa-san!” 

“Ah, yes, what is it?” 

When she enthusiastically leaned forward, she kept her distance— it seems she wasn’t completely careless. Not worrying about that, I told her what my flash of insight was. 

“From before, ‘5×1’ or ‘9×5’…… Hanekawa-san, you’ve been presenting the multiplication table using the numbers written down the sides as the norm right? Starting from the numbers on the side followed by the numbers on the top right?” 

“Hmm. Hmmmm. Because that’s how times table work, right? There’s the “one times table,” the “two times table”… I’ve also recently started to realize that I myself am most likely an eccentric, but isn’t this how everyone does it?” 

“Certainly, the times tables are like that. Everyone does it like that, even me. But, Hanekawa-san, shogi is different. It’s not the numbers running down the ranks that are read first, it’s the numbers running across the files. ‘P-26’, ‘R-58’, like that.” And that’s not all, I said. 

Using the same chalk that I had borrowed, this time I added to the first board that was drawn—I desperately added the vertical and horizontal progressions. 

“The line-up of the numbers written across the top is the exact opposite on a shogi board and a multiplication table.” 

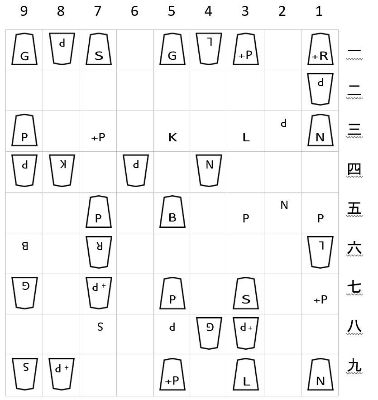
On a shogi board, “1-9” go from right to left. 

On a multiplication table, “1-9” go from left to right. 

In this slight difference, there was too large of a difference. 

On a hand-drawn board the number progression would be omitted, and while it was obvious that Hanekawa-san, who wasn’t familiar with shogi, wouldn’t have noticed, to a pro, it was of grave importance not to mix the numbers up—because if the girl who was her letter exchange partner was putting on airs of being a competent shogi player, she wouldn’t make such a careless mistake. 

So what comes next? What happens? 

“So what?” 

“So—it gets turned upside down, right?” 

Hanekawa-san’s eyes glowed with a fiery light. Not just bright, they were blazing. 

If you let me say one of my typical insensitive remarks, those eyes were dangerous—that wasn’t the look of someone who was doing it for their fabulous friend or to help someone in trouble. 

Compared to that suspicious sparkle, the look in Oikura-san’s eyes in her portrait had to be exaggerated. Now that I thought about it, it was downright cute.  

People say that one’s eyes light up, but somehow, at this moment, Hanekawa-san’s eyes appeared to be shining in gold. 

Like a cat’s—no. 

Like a devil’s. 

Flip them around? 

“That’s why we have to invert the multiplication table and think of it like this—to the very end this is a shogi board. The numeric value of the odd numbers that are covered and the ones that aren’t change— like,” 

As if she were possessed, Hanekawa-san started to draw a new board on the ground like she was digging into it. Since I was borrowing one of her two pieces of chalk, this time she was drawing with just her right hand. 

That was faster. 

That way was faster? “This!” 

Her speed drawing finished, Hanekawa-san turned in my direction. “The odd numbers covered by the black player’s pieces are: 

1 × 一 = 1,     1 × 三 = 3,     3 × 一 = 3,     1 × 五 = 5, 

5 × 一 = 5,     1 × 七 = 7,     7 × 一 = 7,     1 × 九 = 9, 

9 × 一 = 9,     3 × 三 = 9,     3 × 五 = 15,     5 × 三 = 15, 

3 × 七 = 21,     7 × 三 = 21,     5 × 五 = 25,     3 × 九 = 27, 9 × 三 = 27,     5 × 七 = 35,     7 × 五 = 35,     5 × 九 = 45, 

that’s twenty pieces, and the five spaces not covered by pieces are 

9 × 五 = 45,     7 × 七 = 49,     7 × 九 = 63,     9 × 七 = 63,     and 

9 × 九 = 81!” 

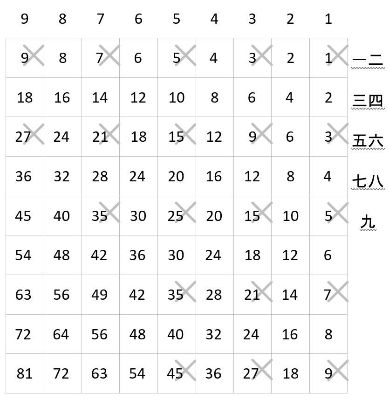
Even as she kept speaking on and on, vigorously and quickly, though with an unbelievable fluency, even though it was obvious if you looked at her drawing—then, in the end, all that changed were the odd numbers that weren’t covered by pieces? 

That’s not it. The meaning also changed. 

A clear difference was born between the odd numbers that were covered and those that weren’t covered—you could draw a definite line between them. 

The five odd numbers that weren’t covered, 45, 49, 63, 63, 81, among the odd numbers on the inverted multiplication table, when you arranged the numbers by value, they were the last five. 

There was a rule. 

Before, when Hanekawa-san was considering a standard multiplication table, she was suspicious of what the difference was between the “5” of “1 × 5 = 5” and the “5” of “5 × 1 = 5”, between the one that was covered and the one that was uncovered. But if you compare it to this rule, the answer to that question was also obvious.  

On the most recent table that was “45”, in other words, the “45” from “5 × 九 = 45” and the “45” from “9 × 五 = 45”. If you change the question to why the former was covered and the latter wasn’t covered—it was simply the result of the ninth rank coming later in the order than the fifth rank. Since the number written across the top was said first, even though it wasn’t the “rank”…… 

“When we adjust it, on the inverted multiplication table of the twenty-five odd numbers, as before four-fifths are covered and the remaining one-fifth are uncovered.” Four-fifths of the odd numbers. 

That was the message sent to Oikura-san—Hanekawa-san took a deep breath and curled up into a ball, as if she were hanging her head. 

That blazing glow in her eyes had also gone out before I knew it. 

 It was as if the evil spirit that was possessing her had left. 

No, it’s not as if human eyes just suddenly start glowing gold, it was probably just a trick of the light. Hmm? 

No, if I just leave her alone, the vigorous Hanekawa-san would lie down on that spot sprawled out, but even if you say it looked like everything was resolved…… 

Aren’t we still in the middle of solving this riddle? 

“Nope. Thanks to you, Kiriyama-kun, I’ve already got the whole thing worked out—I wonder if you wouldn’t mind going over it together with me?” 

Together or whatever, just ending things here after coming this far, gave me indigestion. 

“From here on out it isn’t shogi or math anymore—what Kiriyama-kun called a quick-wit. Or wordplay. That might be our specialty.” Our? 

“ ‘Four-fifths of the odd numbers’. That’s the message the penpal wanted to send to Oikura-san. If possible two-thirds would have been more beautiful, but you can’t divide twenty-five by three. So they decided to go with the second best option of four-fifths.” 

Hanekawa-san kept saying the math talk was over, but eventually a new fraction came out—they want two-thirds but settled for fourfifths? No matter what they would equal mathematically. 

Then if not mathematically? In Japanese? 

Hanekawa-san (and friends?) was a specialist in Japanese? 

No, she didn’t say Japanese—she said words. 

Wordplay. 

Come to think of it, Hanekawa-san noticed the comparison between the shogi board and a multiplication table from the association of shishi from the Lion King Tournament and 4 × 4 = 16. 

“……” 

I didn’t get the hint for only a second, leaving aside wordplay for the moment, if you limit it to just reading—that was the province of pros (also leaving aside the point of not being able to read the air).   

Odd numbers. 

If you take the two-character compound for “odd” 奇数 and rewrite it in hiragana, then it would be the three characters きすう—then what if you were to rewrite that to get five characters? It’s obvious. 

Using the Latin alphabet, it would be “kisuu”. 

If it’s like this, then two-thirds and four-fifths are equal. 

The first two characters of the three. 

And the first four characters of the five. 

Namely— 

“Huh, what? ‘kisu’, ‘kiss’?” 

“Yeah. Still, this is plenty, charming and exciting, but if you want to make a girl say that, and you want them to follow the proper order of things, add one more contrivance. One more bit of fiddling, or rather, twisting.” 

In contrast to me, who was absolutely perplexed at this out of place answer that we derived, in the end Hanekawa-san once more pointed at the first board. 

“The board that shows the white and black players—in this case, if we look at it from Oikura-san’s perspective, all of the black player’s, the pen-pal’s, pieces look upside down—if so, Kiriyama-kun, don’t you feel the most appropriate move is to take our derived answer and flip it over?” 

Flip over “kiss”? 

Flip it over—“suki”, “love”? 

--------------------

11  The word for “zero”, 零 (rei), is the same character as Kiriyama’s first name.

12  Shimada Kai is a professional shogi player, and a central figure and role model to Kiriyama.